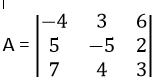Determinan Matriks

 Halo semua, perkenalkan saya Rafi Ramadhan Ghifari dengan NIM 202231013 prodi Teknik Informatika fakultas Telematika Energi kelas A. Pada kesempatan kali ini, saya akan membahas mengenai Determinan Matriks. Mau tahu seperti apa ?? Yuk simak berikut ini !!.

A. Pengertian

Fungsi determinan matriks bujur sangkar A dinyatakan dengan det(A) = |A|, didefinisikan sebagai penjumlahan hasil kali elementer elemen-elemen bertanda A. 

•     Kasus n = 1

A = [a], det(A) = |a| = a

• Kasus n = 2

• Kasus n = 3, metode Sarrus

B. Metode Ekspansi Laplace

Andaikan A = [aij] dengan ordo matriks (nxn). Minor elemen matriks A baris ke-i dan kolom ke-j (a-ij) ditulis menjadi Mij dan didefinisikan sebagai determinan matriks berordo (n-1)x(n-1) yang diperoleh dari A dengan cara menghilangkan baris ke-i dan kolom ke-j. Kofaktor elemen matriks A baris ke-i dan kolom ke-j ditulis C-ij dan didefinisikan sebagai : 

Cij = (-1)i+j Mij.

1. Contoh Pertama :

     2. Contoh Kedua : 

M42 determinan matriks berordo (3x3) baris ke-4 dan kolom ke-2 dari matriks dihilangkan. 

C. Determinan Metode Ekspansi Laplace

Untuk n = 1 :

det(A) = | A | = |a11| =a11, untuk n lebih dari sama dengan 2 determinan matriks A diberikan oleh, 

D. Determinan Metode Chio

Dikenal dengan rumus menghitung determinan dengan mereduksi ordo atau ukuran matriks. Reduksi ordonya dapat pula menggunakan elemen matriks yang lain, tidak harus a11. 

Contoh : 

dikarenakan a11 = -4 dan n = 3, maka :

Mungkin ini yang dapat saya sampaikan, jika ada kesalahan mohon dimaafkan karena yang benar hanyalah milik Allah swt.