Nama : Rafi Ramadhan Ghifari
NIM : 202231013
Kelas : A
Program Studi : Teknik Informatika
Pada kesempatan kali ini saya akan menyampaikan materi terkait Basis dan Basis Ruang Vektor
A. Pengertian Basis
Andaikan V adalah sembarang ruang vektor dan S = {u1, u2,…,un} adalah himpunan berhingga vektor-vektor pada V, S dikatakan basis untuk ruang V jika S bebas linier dan S membangun V.
B. Pengertian Dimensi
Sebuah ruang vektor dikatakan berdimensi berhingga, jika ruang vektor V mengandung sebuah himpunan berhingga vektor S = {u1, u2,…,un} yang membentuk basis. Dimensi sebuah ruang vektor V yang berdimensi berhingga didefinisikan sebagai banyaknya vektor pada basis V.
Contoh :
Misalkan B={i,j,k} dengan i=[1,0,0], j=[0,1,0], dan k=[0,0,1]. B adalah basis baku untuk R³. Karena banyaknya vektor yang membentuk basis B adalah 3, maka R³ berdimensi tiga.
C. Ruang Baris, Ruang kolom dan Nul
Misalkan matriks m x n dengan vektor :
Pada Rn yang dibentuk dari baris-baris, maka matriks A disebut dengan vektor baris.
Sedangkan pada Rm yang terbentuk dari kolom-kolom matriks A disebut dengan vektor kolom.
Definisi :
Jika A adalah matriks 𝑚 × 𝑛 maka subruang dari 𝑅𝑛 yang direntang oleh vektor-vektor baris dari A disebut ruang baris dari A, dan subruang dari 𝑅𝑚 yang direntang oleh vektor-vektor kolom dari A disebut ruang kolom dari A. Ruang solusi dari sistem persamaan yang homogen 𝐴𝑥 = 0 yang merupakan subruang dari 𝑅𝑛 disebut ruang nul dari A.
Teorema 1 :
Jika A dan dan B adalah matriks-matriks yang ekuivalen baris, maka
• Suatu himpunan vektor-vektor kolom dari dari A tertentu adalah bebas linear jika dan hanya jika vektor – vektor kolom yang bersesuaian dari B adalah bebas linear
• Suatu himpunan vektor-vektor kolom kolom dari A tertentu membentuk suatu basis untuk ruang kolom dari A jika dan hanya jika vektor -vektor kolom yang bersesuaian dari B membentuk suatu basis untuk ruang kolom dari B.
Teorema 2 :
Dan jika suatu matriks R berada dalam bentuk eselon baris, maka vektor vektor baris dengan 1 utama membentuk suatu basis untuk ruang baris dari R dan Vektor-vektor kolom dengan 1 utama dari vektor-vektor baris membentuk suatu basis untuk ruang kolom dari R.
Jika A adalah matriks sebarang, maka ruang baris dan ruang kolom dari A memiliki dimensi yang sama.
Rank = Dimensi umum dari ruang baris dan ruang kolom.
Nulitas = Dimensi ruang null dari A.
Jika A adalah matriks dengan n kolom, maka :
Rank (A) + Nulitas (A) = n










.jpg)
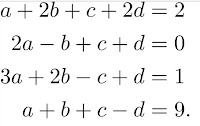






.JPG)





